ASTC Compression Accleration Using CUDA

Overview

ASTC is a fixed-rate, lossy texture compression system that is designed to offer an unusual degree of flexibility and to support a very wide range of use cases, while providing better image quality than most formats in common use today.

However, ASTC need to search a lot of candidate block modes to find the best format. It takes a lot of time to compress the texture in practice. Since the texture block compression is not relevant to each other at all, we can compress the texture parallelly with GPU.

In our project, we compress the texture with Cuda. The compression algorithm is based on the arm astc-enc implementation. It’s a CPU-based compression program. We port arm-astc to GPU and make full use of the cuda to acclerate the texture compression.

A naive implementation of GPU ASTC compression is compressing the ASTC texture block per thread, that is, task parallel compression. Since the block compression task is heavy and uses many registers, the number of active warps is low, which causes low occupancy. To make full use of the GPU, we use data parallel to compress the ASTC block per CUDA block. It splits the “for loop” task into each thread and shares the data between lanes by warp shuffle as possible as we can.

The astc-enc implementation has a large number of intermediate buffers during candidate block mode searching, which has little performance impact on CPU-based implementations, but has a significant impact on GPU-based implementations. We have optimized this algorithm by in-place update, which removes the intermediate buffer.

CPU Based Implementation

Bounded Integer Sequence Encoding

ASTC uses BISE to encode color end points and color weights. We introduce BISE first since it is the basis of the ASTC compression algorithm.

Both the weight data and the endpoint color data are variable width, and are specified using a sequence of integer values. The range of each value in a sequence (e.g. a color weight) is constrained.

Since it is often the case that the most efficient range for these values is not a power of two, each value sequence is encoded using a technique known as “integer sequence encoding”. This allows efficient, hardware-friendly packing and unpacking of values with non-power-of-two ranges.

In a sequence, each value has an identical range. The range is specified in one of the following forms:

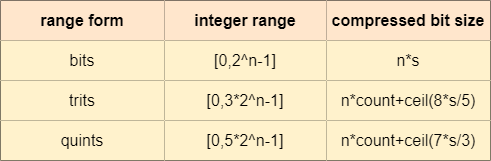
There are 21 quant methods in ASTC, including 6 quints quant forms, 7 trits quant forms and 8 bits quant forms.

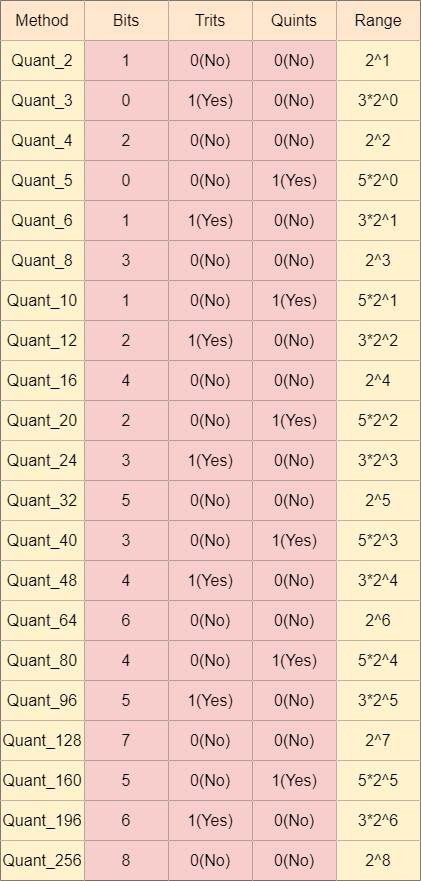
For example, assume we have 3 integer values: 30, 50 and 70. The minimum range of quant formats among these values is Quant_80. The binary formats of these values are: 001 1110(30), 011 0010(50) and 100 0110(70). The total bits size before quantization is 21 = 7 * 3.

The binary format of value 80 is 101 0000. We split it into two parts, the higher parts 101 and lower parts 0000. The possible values of the higher parts are from 000 to 101, whose total number is 5, so Quant 80 is a quints form.

The higher parts of 30, 50 and 70 are [001, 011, 100]. In the Quant 80 method, the total possible number is 5, so the number of possible combinations of [001, 011, 100] is 5x5x5 = 125. We can precompute these possible values into a table and use the 7 bit value to index the table. The result is a 2 bit saving for these integers.

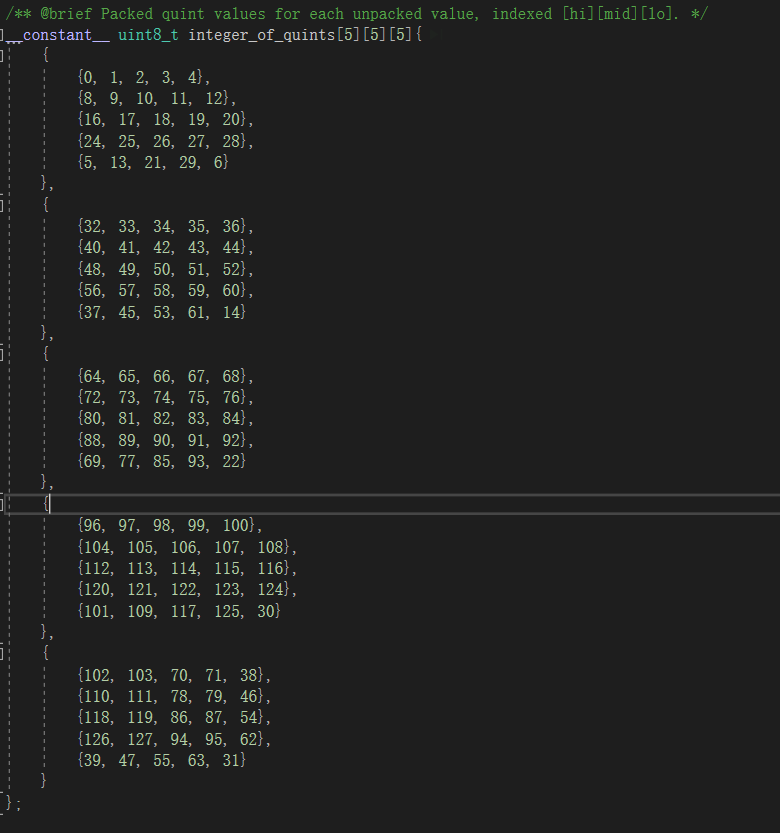
Higher parts [001, 011, 100] equal to [1,3,4]. Using index [1][3][4] to search the below quints table, we get the compressed value:11, which is 1011 in binary format. The compressed result is [000 1011](higher parts),[1110],[0010],[0110](lower parts) with size 19.

Generate Block Mode

ASTC uses 10 bits to store block modes, which means it has 2^11(2048) kind of possible choices. Given an ASTC compression format, some block modes may be invalid. For example, ASTC 4x4 compression format will never use a block mode with 6x6 texel weights. So we search for valid block modes and store the results in a global block mode table. In order to reduce the computation cost of block mode search, arm-astc reordered the block modes so that the better block mode has a higher priority.

Search block mode from 000000000(0) to 1111111111(2048).

1
2
3
4
for (unsigned int i = 0; i < 2048; i++)
{
    // ......
}

The Block Mode field specifies the width, height and depth of the grid of weights, what range of values they use, and whether dual weight planes are present.

For 2D blocks, the Block Mode field is laid out as follows:

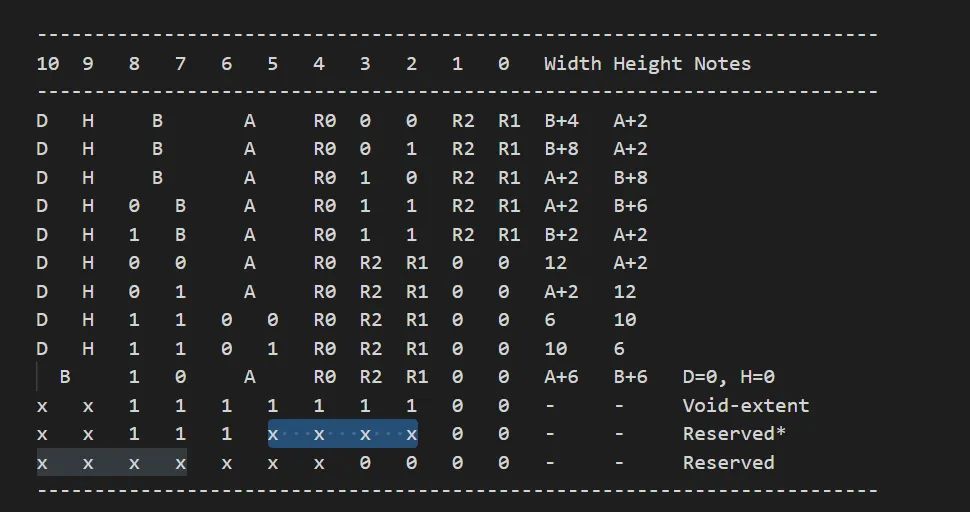
The D bit is set to indicate dual-plane mode.

The A/B bits indicate the block weight size.

The weight ranges are encoded using a 3 bit value R(R0,R1 and R2), which is interpreted together with a precision bit H, as follows:

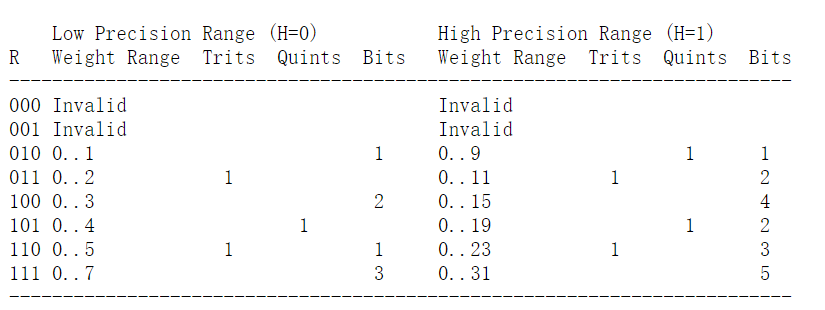
Decode the R,H,D, weight sizes x and y from the bits.

1
2
3
4
5
6
7
uint8_t R0 = (block_mode >> 4) & 1;
uint8_t H = (block_mode >> 9) & 1;
uint8_t D = (block_mode >> 10) & 1;
uint8_t A = (block_mode >> 5) & 0x3;

x_weights = xxxxxx;
y_weights = xxxxxx;

Skip the block mode if the qunat weight size is larger than the compression block size.

1
2
3
4
if (!valid || (x_weights > x_texels) || (y_weights > y_texels))
{
	continue;
}

valid block mode:

Compute Ideal Color And Weights

Color Encoding

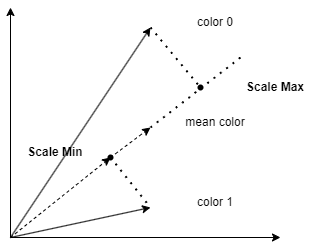
Each compressed block stores the end-point colors for a gradient, and an interpolation weight for each texel which defines the texel’s location along that gradient. During decompression the color value for each texel is generated by interpolating between the two end-point colors, based on the per-texel weight.

We sum up the relative colors in the positive R, G, and B directions and calculate the sum of direction lengths.

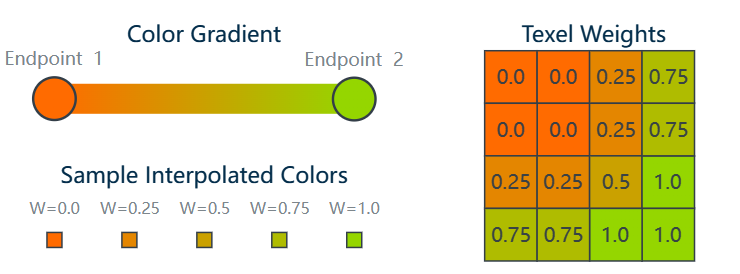
Endpoints Computation

Compute the mean color value and the main color direction first. There are many main direction calculation method. We use max accumulation pixel direction as the main direction, which is the same as the arm-astc implementation. We sum up the relative colors in the positive R, G, and B directions and calculate the sum of direction lengths.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
float4 sum_xp(0.0);
float4 sum_yp(0.0);
float4 sum_zp(0.0);
float4 sum_wp(0.0);

for (unsigned int i = 0; i < blk.texel_count; i++)
{
	float4 texel_datum = make_float4(blk.data_r[i], blk.data_g[i], blk.data_b[i], blk.data_a[i]);
	texel_datum = texel_datum - blk.data_mean;

	sum_xp += (texel_datum.x > 0) ? texel_datum : make_float4(0);
	sum_yp += (texel_datum.y > 0) ? texel_datum : make_float4(0);
	sum_zp += (texel_datum.z > 0) ? texel_datum : make_float4(0);
	sum_wp += (texel_datum.w > 0) ? texel_datum : make_float4(0);
}

float prod_xp = dot(sum_xp, sum_xp);
float prod_yp = dot(sum_yp, sum_yp);
float prod_zp = dot(sum_zp, sum_zp);
float prod_wp = dot(sum_wp, sum_wp);

Use the maximum sum direction as the main direction

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
float4 best_vector = sum_xp;
float best_sum = prod_xp;

if (prod_yp > best_sum)
{
	best_vector = sum_yp;
	best_sum = prod_yp;
}

if (prod_zp > best_sum)
{
	best_vector = sum_zp;
	best_sum = prod_zp;
}

if (prod_wp > best_sum)
{
	best_vector = sum_wp;
	best_sum = prod_wp;
}

dir = best_vector;

Interpolation Weight Computation

Project the color into the main direction for each texel and find the minimum and maximum projected value by the way.

1
2
3
4
5
6
7
8
9
10
11
12
line4 line{ blk.data_mean, length_dir < 1e-10 ? normalize(make_float4(1.0)) : normalize(dir) };

for (unsigned int j = 0; j < blk.texel_count; j++)
{
	float4 point(blk.data_r[j], blk.data_g[j], blk.data_b[j], blk.data_a[j]);
	float param = dot(point - line.a, line.b);

	ei.weights[j] = param;

	lowparam = fmin(param, lowparam);
	highparam = fmax(param, highparam);
}

Calculate the end points based on the min/max projected color.

1
2
ei.ep.endpt0 = line.a + line.b * lowparam;
ei.ep.endpt1 = line.a + line.b * highparam;

Normalize the weight range into 0 to 1:

1
2
3
4
5
6
7
8
9
float length = highparam - lowparam;
float scale = 1.0f / length;

for (unsigned int j = 0; j < blk.texel_count; j++)
{
	float idx = (ei.weights[j] - lowparam) * scale;
	idx = clamp(idx, 0.0, 1.0);
	ei.weights[j] = idx;
}

before color projection:

after color projection:

Compute Weight Quant Error

Compute the quant errors for each candidate block mode. Get the Quant method from the block mode and quantize the weights. After that, unquant the result by look up the precomputed quant map table. It should be noticed that the maximum color weight Quant method is Quant 32 and the maximum color end points Quant method is Quant 256.

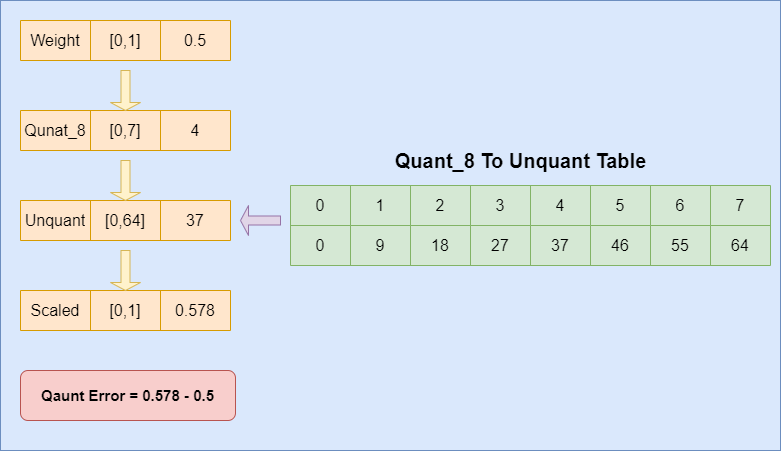
Accumulate the weight quantization error for the texel weights in the block.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
float error_summa = 0;
for (unsigned int i = 0; i < bsd.texel_count; i++)
{
	// Load the weight set directly, without interpolation
	float current_values = weight_quant_uvalue[i];

	// Compute the error between the computed value and the ideal weight
	float actual_values = eai.weights[i];
	float diff = current_values - actual_values;

	float error = diff * diff;
	error_summa += error;
}
return error_summa;

weights quant error result:

Compute Endpoint Quant Error

The next step is to search for the best K candidate end point format as we have the quant error of each block mode.

CEM

CEM is the color endpoint mode field, which determines how the Color Endpoint Data is encoded. Here is the CEM layout for single-partition block layout:

In single-partition mode, the Color Endpoint Mode (CEM) field stores one of 16 possible values. Each of these specifies how many raw data values are encoded, and how to convert these raw values into two RGBA color endpoints. They can be summarized as follows:

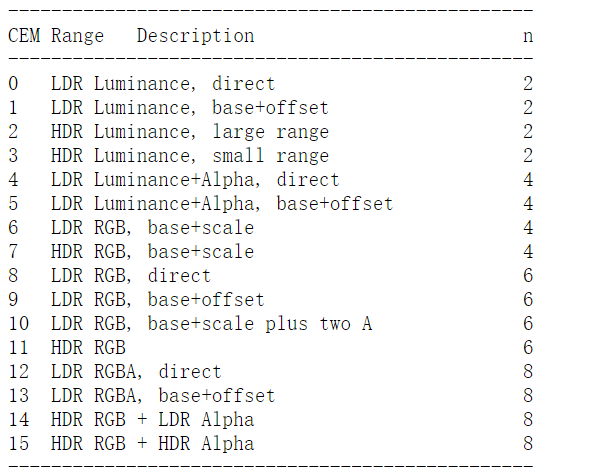
ASTC has 16 color end point modes. To store the end points, Modes 0 to 3 use two integers, Modes 4 to 7 use four integers, Modes 7 to 11 use six integers, and Modes 12 to 15 use eight integers. In our implementation, we only support six modes: mode 0, mode 4, mode 6, mode 8, mode 10 and mode 12.

Decode the different LDR endpoint modes as follows:

1.Mode 0 LDR Luminance, direct:

1
2
e0=(v0,v0,v0,0xFF); 
e1=(v1,v1,v1,0xFF);

2.Mode 4 LDR Luminance+Alpha,direct:

1
2
e0=(v0,v0,v0,v2);
e1=(v1,v1,v1,v3);

3.Mode 6 LDR RGB, base+scale

1
2
e0=(v0*v3>>8,v1*v3>>8,v2*v3>>8, 0xFF);
e1=(v0,v1,v2,0xFF);

4.Mode 8 LDR RGB, Direct

1
2
3
4
5
6
7
8
9
10
11
12
s0= v0+v2+v4; 
s1= v1+v3+v5;
if (s1>=s0)
{
	e0=(v0,v2,v4,0xFF);
    e1=(v1,v3,v5,0xFF); 
}
else 
{ 
	e0=blue_contract(v1,v3,v5,0xFF);
    e1=blue_contract(v0,v2,v4,0xFF); 
}

5.Mode 10 LDR RGB, base+scale plus two A

1
2
e0=(v0*v3>>8,v1*v3>>8,v2*v3>>8, v4);
e1=(v0,v1,v2, v5)

6.Mode 12 LDR RGBA, direct

1
2
3
4
5
6
7
8
9
10
11
s0= v0+v2+v4; s1= v1+v3+v5;
if (s1>=s0)
{
	e0=(v0,v2,v4,v6);
    e1=(v1,v3,v5,v7); 
}
else 
{
	e0=blue_contract(v1,v3,v5,v7);
    e1=blue_contract(v0,v2,v4,v6); 
}

Then, we estimate the error of each end point mode. Color end point modes can be classified into 3 types: luminance representation, scale representation and RGB representation. In astc-enc, the error estimation of luminance representation is the sum of the distances to vector normalize(lumi,lumin,lumin) = float3(0.57,0.57,0.57). Scale representation error estimation is the sum of the distance to vector normalize(EndPointA + EndPointB).

1
2
3
4
5
6
samec_rgb_lines.a = make_float4(0);
samec_rgb_lines.b = normalize_safe(avg);

float val = 0.577350258827209473f;
luminance_plines.amod = make_float4(0);
luminance_plines.bs = make_float4(val, val, val, 0.0f);

Calculate and accumulate the scale and luminance error of each texel:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// Compute same chroma error - no "amod", its always zero
param = data_r * samec_bs0+ data_g * samec_bs1 + data_b * samec_bs2;

dist0 = (param * samec_bs0) - data_r;
dist1 = (param * samec_bs1) - data_g;
dist2 = (param * samec_bs2) - data_b;

error = dist0 * dist0 + dist1 * dist1 + dist2 * dist2;

samec_err += error;

// Compute luma error - no "amod", its always zero
param = data_r * l_bs0 + data_g * l_bs1 + data_b * l_bs2;

dist0 = (param * l_bs0) - data_r;
dist1 = (param * l_bs1) - data_g;
dist2 = (param * l_bs2) - data_b;

error = dist0 * dist0 + dist1 * dist1 + dist2 * dist2;

l_err += error;

The endpoint encoding uses 21 quant levels and 4 kinds of integer numbers, resulting in a total candidate format count of 21 * 4. For each quant level, we choose the endpoint format for each kind of integer number.

The error estimation contains six parts: baseline quant error, base quant error RGB, base quant error RGBA, scale error, luminance error, drop alpha error.

1.Baseline quant error is precomputed in a look up table and indexed by quant level.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
__constant__ float baseline_quant_error[21 - QUANT_6]{
	(65536.0f * 65536.0f / 18.0f) / (5 * 5),
	(65536.0f * 65536.0f / 18.0f) / (7 * 7),
	(65536.0f * 65536.0f / 18.0f) / (9 * 9),
	(65536.0f * 65536.0f / 18.0f) / (11 * 11),
	(65536.0f * 65536.0f / 18.0f) / (15 * 15),
	(65536.0f * 65536.0f / 18.0f) / (19 * 19),
	(65536.0f * 65536.0f / 18.0f) / (23 * 23),
	(65536.0f * 65536.0f / 18.0f) / (31 * 31),
	(65536.0f * 65536.0f / 18.0f) / (39 * 39),
	(65536.0f * 65536.0f / 18.0f) / (47 * 47),
	(65536.0f * 65536.0f / 18.0f) / (63 * 63),
	(65536.0f * 65536.0f / 18.0f) / (79 * 79),
	(65536.0f * 65536.0f / 18.0f) / (95 * 95),
	(65536.0f * 65536.0f / 18.0f) / (127 * 127),
	(65536.0f * 65536.0f / 18.0f) / (159 * 159),
	(65536.0f * 65536.0f / 18.0f) / (191 * 191),
	(65536.0f * 65536.0f / 18.0f) / (255 * 255)
};

2.In our implementation, the base quant error of each channel is the same. In astc-enc, the error of each channel can be adjusted by the user.

1
2
3
float base_quant_error_rgb = 3 * blk.texel_count;
float base_quant_error_a = 1 * blk.texel_count;
float base_quant_error_rgba = base_quant_error_rgb + base_quant_error_a;

3.Scale error, luminance error and drop alpha error are computed in the previous step.

4.The final error for each endpoint format is the combination of the above errors.

Take the example of computing the error for the endpoint format encoded by 4 integers using the quant method 7.

The error of mode <RGB base + scale> calculation formula is as follows:
rgbs_alpha_error = base quant error rgba * baseline quant error of quant method 7 + rgb scale error

The error of mode calculation formula:
full_ldr_rgb_error = base quant error rgb * baseline quant error of quant method 7 + alpha drop error

Select the format with the minimum error:

1
2
3
4
5
6
7
8
9
10
if (rgbs_alpha_error < full_ldr_rgb_error)
{
	best_error[i][2] = rgbs_alpha_error;
	format_of_choice[i][2] = FMT_RGB_SCALE_ALPHA;
}
else
{
	best_error[i][2] = full_ldr_rgb_error;
	format_of_choice[i][2] = FMT_RGB;
}

Find The Best Endpoint Quantization Format

Search for all possible combinations of qunat level and color endpoint mode. We can obtain the available number of weight bits from the given block mode. Given the number of available bits and the number of integer, we want to choose the quant level as high as possible to minimize the quantization error. It can be precomputed in a lookup table offline:

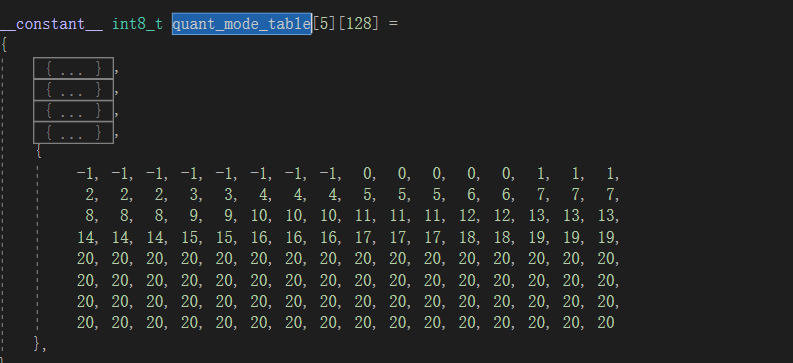
The best quant level can be directly accessed from the lookup table at runtime:

1
int quant_level = quant_mode_table[integer_count][bits_available];

Store the best number of integers that has the minimum error given a block mode.

1
2
3
4
5
6
7
8
9
10
11
for (int integer_count = 1; integer_count <= 4; integer_count++)
{
	int quant_level = quant_mode_table[integer_count][bits_available];

	float integer_count_error = best_combined_error[quant_level][integer_count - 1];
	if (integer_count_error < best_integer_count_error)
	{
		best_integer_count_error = integer_count_error;
		best_integer_count = integer_count - 1;
	}
}

best color endpoint quant format:

Find The Candidate Block Mode

The block mode total error is the sum of the errors that quantify the block texels weights and color endpoint.

1
2
3
4
5
for (unsigned int i = start_block_mode; i < end_block_mode; i++)
{
	float total_error = error_of_best + qwt_errors[i];
	errors_of_best_combination[i] = total_error;
}

We only compute the rough estimation error up to the current step. The next step is to compute the exact error given a block mode. We need to compress and quantify the block texels for each block mode. Since it is an expensive process, we choose four candidate block modes based on the block mode estimation error.

For each candidate block mode search iteration, find the block mode with the minimum error combining weight quant error and endpoint quant error, record the candidate block mode index:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for (unsigned int i = 0; i < 4; i++)
{
	int best_error_index(-1);
	float best_ep_error(ERROR_CALC_DEFAULT);

	for (unsigned int j = start_block_mode; j < end_block_mode; j++)
	{
		float err = errors_of_best_combination[j];
		bool is_better = err < best_ep_error;
		best_ep_error = is_better ? err : best_ep_error;
		best_error_index = is_better ? j : best_error_index;
	}

	best_error_weights[i] = best_error_index;
	errors_of_best_combination[best_error_index] = ERROR_CALC_DEFAULT;
}

Find The Actually Best Mode

Iterate over the 4 candidate block modes to find which one is actually best by quantifying the block and computing the error after unquantifying.

RGB Scale Format Quantification

As we quantize and decimate weights the optimal endpoint colors may change slightly, so we must recompute the ideal colors for a specific weight set.

RGB scale format contains two parts: the base endpoint and the scale factor.

1
2
e0=(v0*v3>>8,v1*v3>>8,v2*v3>>8, 0xFF);
e1=(v0,v1,v2,0xFF);

Compute the scale direction by normalizing the mean color and projecting the block texels to the scale direction. In addition, recording the min/max scale factor.

Compute the base color and scale factor based on the scale direction and scale maximum factor.

1
2
3
4
5
float scalediv = scale_min / max(scale_max, 1e-10f);
scalediv = clamp(scalediv,0.0,1.0);

float4 sds = scale_dir * scale_max;
rgbs_vectors = make_float4(sds.x, sds.y, sds.z, scalediv);

Quantify Endpoints

Endpoint quantification is the same as interpolation weight quantification. There are only 17 possible quant levels and 255 possible values for each color channel. Therefore, the results can be stored in a precomputed table.

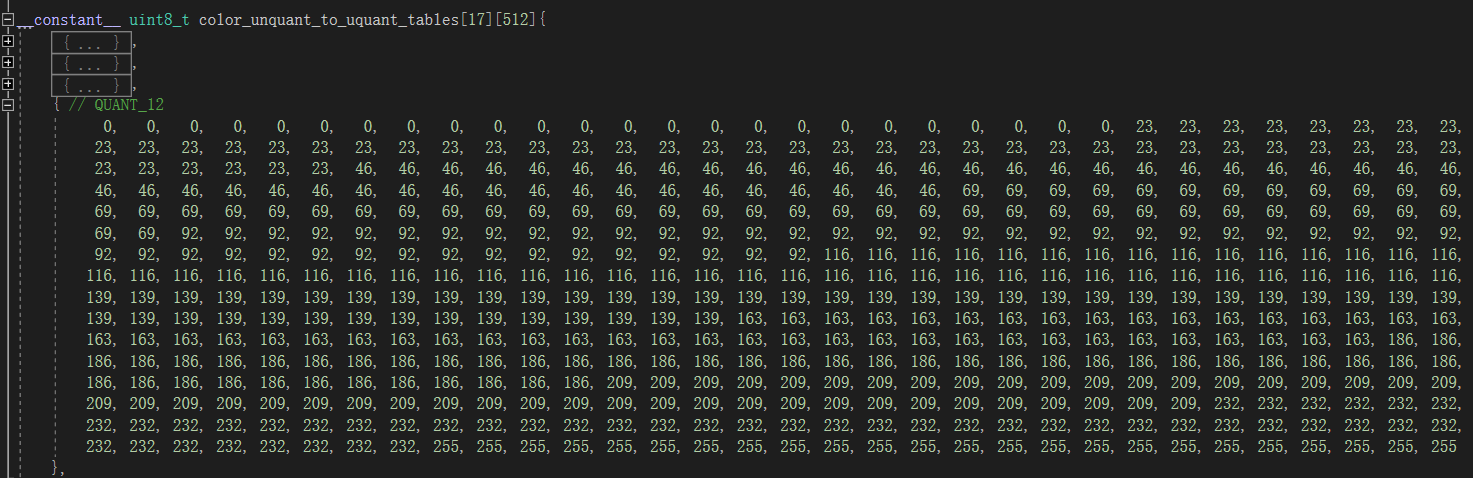
Error Metric

Given a candidate block mode, interpolate the texel color using quantized color endpoints and quantized weights. Compute the color difference and estimate the error using the squared error metric.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for (unsigned int i = 0; i < texel_count; i++)
{
	// quantized weight * quantized endpoint

	float color_error_r = fmin(abs(color_orig_r - color_r), float(1e15f));
	float color_error_g = fmin(abs(color_orig_g - color_g), float(1e15f));
	float color_error_b = fmin(abs(color_orig_b - color_b), float(1e15f));
	float color_error_a = fmin(abs(color_orig_a - color_a), float(1e15f));

	// Compute squared error metric
	color_error_r = color_error_r * color_error_r;
	color_error_g = color_error_g * color_error_g;
	color_error_b = color_error_b * color_error_b;
	color_error_a = color_error_a * color_error_a;

	float metric = color_error_r + color_error_g + color_error_b + color_error_a;

	summa += metric;
}

Find the block mode with the minimum block error.

1
2
3
4
5
6
if (errorval < best_errorval_in_scb)
{
	best_errorval_in_scb = errorval;
	workscb.errorval = errorval;
	scb = workscb;
}

Block Encode

Having found the best block mode with the minimum error, we can finally encode the block.

Below is a layout of the ASTC block. It contains the following parts in order: texel weight data, color endpoint data, color endpoint mode, extra data and block mode data.

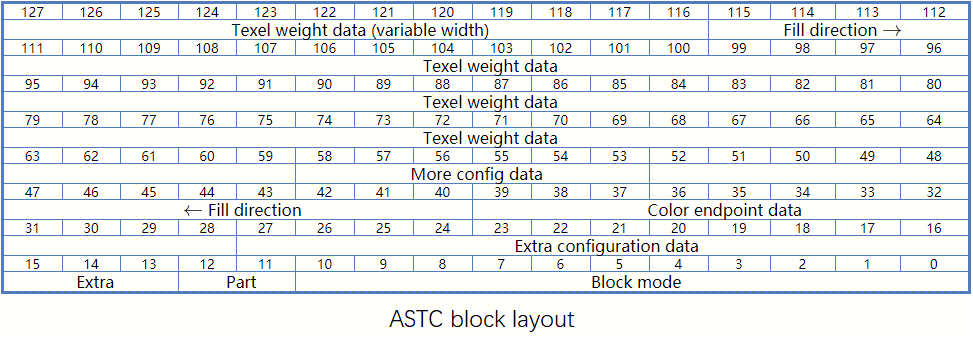
For texel weight, we scale the value based on the quant level of the best block mode. In order to improve the decoding efficiency, ASTC scrambles the order of the decoded values relative to the encoded values, which means that it must be compensated for in the encoder using a table.

1
2
3
4
5
6
7
8
uint8_t weights[64];
for (int i = 0; i < weight_count; i++)
{
	float uqw = static_cast<float>(scb.weights[i]);
	float qw = (uqw / 64.0f) * (weight_quant_levels - 1.0f);
	int qwi = static_cast<int>(qw + 0.5f);
	weights[i] = qat.scramble_map[qwi];
}

Once unpacked, the values must be unquantized from their storage range, returning them to a standard range of 0- 255.
For bit-only representations, this is simple bit replication from the most significant bit of the value.
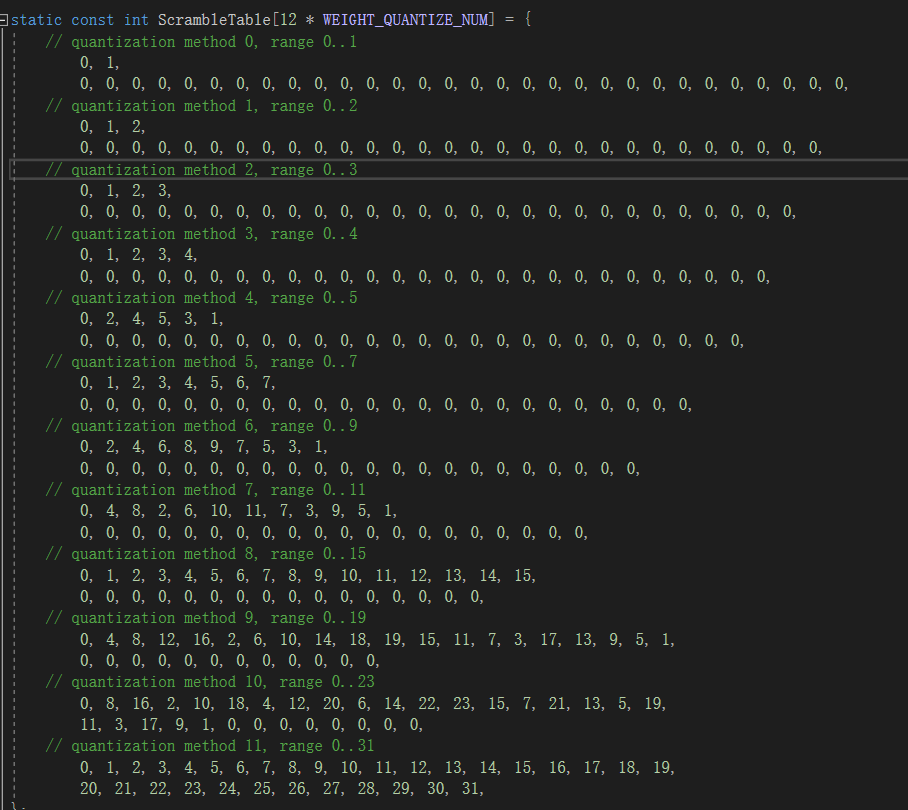
For trit or quint-based representations, this involves a set of bit manipulations and adjustments to avoid the expense of full-width multipliers. This procedure ensures correct scaling, but scrambles the order of the decoded values relative to the encoded values. This must be compensated for using a table in the encoder.

The scramble map table is precomputed:

Next, encode the integer sequence based on the Quant method. Assume that we encode the integer sequence using the Quant_80 method. Quant_80 method quantifies the integer sequence in quints form. Since 5^3 is 125, it is possible to pack three quints into 7 bits (which has 128 possible values), so a quint can be encoded as 2.33 bits.

We split the integer into higher and lower parts and pack three integers’ higher parts into seven bits. The result is precomputed and stored in a lookup table.

1
2
3
4
5
unsigned int i2 = input_data[i + 2] >> bits;
unsigned int i1 = input_data[i + 1] >> bits;
unsigned int i0 = input_data[i + 0] >> bits;

uint8_t T = integer_of_quints[i2][i1][i0];

Then, pack the result with the lower part of the integer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Element 0
pack = (input_data[i++] & mask) | (((T >> 0) & 0x7) << bits);
write_bits(pack, bits + 3, bit_offset, output_data);
bit_offset += bits + 3;

// Element 1
pack = (input_data[i++] & mask) | (((T >> 3) & 0x3) << bits);
write_bits(pack, bits + 2, bit_offset, output_data);
bit_offset += bits + 2;

// Element 2
pack = (input_data[i++] & mask) | (((T >> 5) & 0x3) << bits);
write_bits(pack, bits + 2, bit_offset, output_data);
bit_offset += bits + 2;

The color endpoint packing is the same as the texel weight packing.

GPU Based Implementation

There are two ways to accelerate ASTC block compression: task parallel and data parallel. The task parallel is compressing the texture block per thread. The task parallel for ASTC block compression is heavy and uses many registers. This means that the number of active warps is low and we have low occupancy. Therefore, we can’t make full use of GPU for task parallel.

For data parallel, we compress the ASTC block per cuda block. The GPU-based implementation references the CPU implementation. It splits the “for loop” task into each thread and shares the data between lanes by warp shuffle as possible as we can. For those data that can’t be efficiently shared by warp shuffle, we use shared memory to exchange the data.

Compute Endpoints

The first step is computing the best projection direction for the current block. Before this step, we load the image pixel data per thread and compute the mean pixel data by warp reduce sum operation. Then we broadcast the mean data to the whole warp.

Since the ASTC format 4x4 only has 16 texels to compress and the warp size on N-card is 32, we should mask the lanes used for block texels loading and sum operation.

1
unsigned mask = __ballot_sync(0xFFFFFFFFu, tid < BLOCK_MAX_TEXELS);

We use the max accumulation direction method to compute the best direction, which is the same as the CPU-based implementation. Each lane computes the offset direction relative to the mean block color. Then, we perform warp reduce to compute the sum of the offsets in the xyz direction.

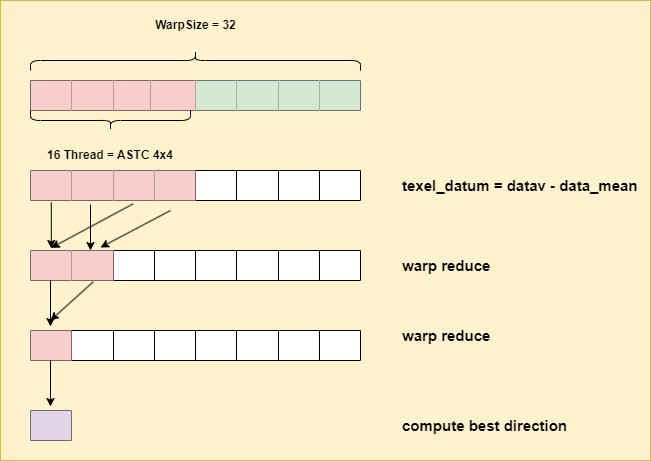
If the lane ID is 0, compute and normalize the best direction based on the length of the sum of offsets in each direction.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
__inline__ __device__ float3 compute_avgs_and_dirs_3_comp(float3 datav,float3 data_mean, uint32_t lane_id, unsigned mask)
{
	float3 safe_dir;
	float3 texel_datum = datav - data_mean;

	float3 valid_sum_xp = (texel_datum.x > 0 ? texel_datum : float3(0, 0, 0));
	float3 valid_sum_yp = (texel_datum.y > 0 ? texel_datum : float3(0, 0, 0));
	float3 valid_sum_zp = (texel_datum.z > 0 ? texel_datum : float3(0, 0, 0));

	float3 sum_xp = warp_reduce_vec_sum(mask, valid_sum_xp);
	float3 sum_yp = warp_reduce_vec_sum(mask, valid_sum_yp);
	float3 sum_zp = warp_reduce_vec_sum(mask, valid_sum_zp);

	if (lane_id == 0)
	{
		float prod_xp = dot(sum_xp, sum_xp);
		float prod_yp = dot(sum_yp, sum_yp);
		float prod_zp = dot(sum_zp, sum_zp);

		float3 best_vector = sum_xp;
		float best_sum = prod_xp;

		if (prod_yp > best_sum)
		{
			best_vector = sum_yp;
			best_sum = prod_yp;
		}

		if (prod_zp > best_sum)
		{
			best_vector = sum_zp;
			best_sum = prod_zp;
		}

		if ((best_vector.x + best_vector.y + best_vector.z) < 0.0f)
		{
			best_vector = -best_vector;
		}

		float length_dir = length(best_vector);
		safe_dir = (length_dir < 1e-10) ? normalize(make_float3(1.0)) : normalize(best_vector);
	}
	return safe_dir;
}

Compute the interpolation weight for each block texels. First, broadcast the best direction to the whole warp and project the texel data to the best direction. Then, use __shfl_xor_sync to compute the min/max value. With the min/max value, we can compute the scaled weight and store the result in shared memory.

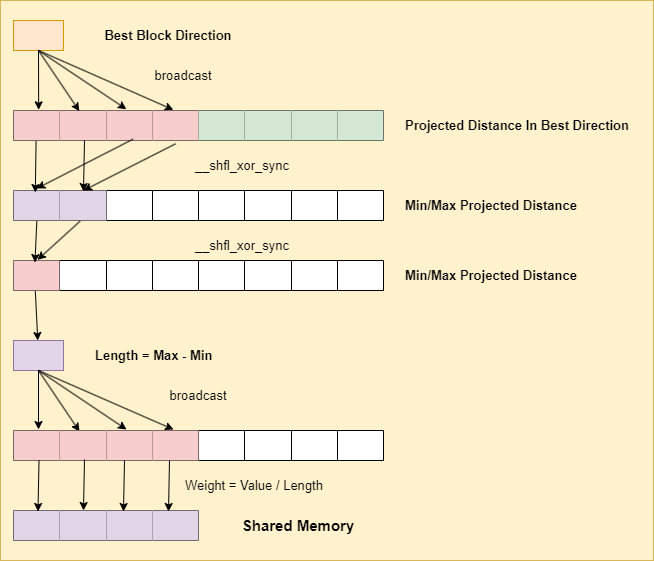
Find The Candidate Block Mode

Our algorithm is based on the arm astc-enc implementation. However, we can’t port the astc-enc to Cuda directly. The astc-enc implementation has a large number of intermediate buffers during candidate block mode searching, which has little performance impact on CPU-based implementations, but has a significant impact on GPU-based implementations.

Here is a brief introduction to how astc-enc finds the candidate block mode:

1.Compute the quant error for each block mode and store the result and quant bits used in an intermediate buffer with the size of 2048 * (float + uint8)

2.For each block mode, compute the best combination with the candidate color quant format. This step has 3 intermediate buffers: best combination error buffer with the size of 2048xfloat, best color quant level buffer with the size of 2048xuint8, best endpoint format with the size of 2048xuint.

3.Choose 4 best candidate block mode and compute the more accurate error.

4.Compress the block using the best block mode

A lot of memory is wasted on the intermediate buffer. We have optimized this algorithm by in-place update, which removes the usage of the intermediate buffer:

1.Maintain a buffer recording the 4 candidate quant formats.

2.Iterate the block mode, compute the interpolation weight quant error, the best combination with the color quant format.

3.Compare with the candidate quant format stored in the step 1. Replace the candidate mode that has a larger error to current quant format.

4.Other steps are the same as the astc-enc implementation.

Prepare

Before iterating 2048 candidate block modes, we need to prepare some infomation used in block quant error computation.

The first one is the color endpoint format error for scale-based color endpoints or luminance-based color endpoints. We compute the errors for each block pixel and sum up the error by warp reduction. Then store the results in shared memory.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// Luminance always goes though zero, so this is simpler than the others
float val = 0.577350258827209473f;
luminance_plines.amod = make_float3(0);
luminance_plines.bs = make_float3(val, val, val);

// Compute uncorrelated error
float param = dot(datav, uncor_rgb_plines.bs);
float3 dist = (uncor_rgb_plines.amod + param * uncor_rgb_plines.bs) - datav;
float uncor_err = dot(dist, dist);

// Compute same chroma error - no "amod", its always zero
param = dot(datav, samec_rgb_plines.bs);
dist = param * samec_rgb_plines.bs - datav;
float samec_err = dot(dist, dist);

// Compute luma error - no "amod", its always zero
param = dot(datav, luminance_plines.bs);
dist = param * luminance_plines.bs - datav;
float l_err = dot(dist, dist);

if (tid == 0)
{
	shared_data_mean = data_mean;
	shared_scale_dir = samec_rgb_lines.b;
}

__syncwarp(mask);

float sum_uncor_err = warp_reduce_sum(mask, uncor_err);
float sum_samec_err = warp_reduce_sum(mask, samec_err);
float sum_l_err = warp_reduce_sum(mask, l_err);

if (lane_id == 0)
{
	shared_rgb_scale_error = (sum_samec_err - sum_uncor_err) * 0.7f;// empirical
	shared_luminance_error = (sum_l_err - sum_uncor_err) * 3.0f;// empirical
}

Color endpoint has 21 quant methods and 4 kind of interger number to quant with total 21*4 possible combinations. We precomputed the result before block mode iteration. Each thread computes one error for one quant method and stores the result in shared memory.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
__inline__ __device__ void compute_color_error_for_every_integer_count_and_quant_level(const block_size_descriptor* const bsd, uint32_t tid)
{
	int choice_error_idx = tid;
	if (choice_error_idx >= QUANT_2 && choice_error_idx < QUANT_6)
	{
		shared_best_error[choice_error_idx][3] = ERROR_CALC_DEFAULT;
		shared_best_error[choice_error_idx][2] = ERROR_CALC_DEFAULT;
		shared_best_error[choice_error_idx][1] = ERROR_CALC_DEFAULT;
		shared_best_error[choice_error_idx][0] = ERROR_CALC_DEFAULT;

		shared_format_of_choice[choice_error_idx][3] = FMT_RGBA;
		shared_format_of_choice[choice_error_idx][2] = FMT_RGB;
		shared_format_of_choice[choice_error_idx][1] = FMT_RGB_SCALE;
		shared_format_of_choice[choice_error_idx][0] = FMT_LUMINANCE;
	}

	float base_quant_error_rgb = 3 * bsd->texel_count;
	float base_quant_error_a = 1 * bsd->texel_count;
	float base_quant_error_rgba = base_quant_error_rgb + base_quant_error_a;

	if (choice_error_idx >= QUANT_6 && choice_error_idx <= QUANT_256)
	{
		float base_quant_error = baseline_quant_error[choice_error_idx - QUANT_6];
		float quant_error_rgb = base_quant_error_rgb * base_quant_error;
		float quant_error_rgba = base_quant_error_rgba * base_quant_error;

		// 8 integers can encode as RGBA+RGBA
		float full_ldr_rgba_error = quant_error_rgba;
		shared_best_error[choice_error_idx][3] = full_ldr_rgba_error;
		shared_format_of_choice[choice_error_idx][3] = FMT_RGBA;

		// 6 integers can encode as RGB+RGB or RGBS+AA
		float full_ldr_rgb_error = quant_error_rgb + 0;
		float rgbs_alpha_error = quant_error_rgba + shared_rgb_scale_error;

		if (rgbs_alpha_error < full_ldr_rgb_error)
		{
			shared_best_error[choice_error_idx][2] = rgbs_alpha_error;
			shared_format_of_choice[choice_error_idx][2] = FMT_RGB_SCALE_ALPHA;
		}
		else
		{
			shared_best_error[choice_error_idx][2] = full_ldr_rgb_error;
			shared_format_of_choice[choice_error_idx][2] = FMT_RGB;
		}

		// 4 integers can encode as RGBS or LA+LA
		float ldr_rgbs_error = quant_error_rgb + 0 + shared_rgb_scale_error;
		float lum_alpha_error = quant_error_rgba + shared_luminance_error;

		if (ldr_rgbs_error < lum_alpha_error)
		{
			shared_best_error[choice_error_idx][1] = ldr_rgbs_error;
			shared_format_of_choice[choice_error_idx][1] = FMT_RGB_SCALE;
		}
		else
		{
			shared_best_error[choice_error_idx][1] = lum_alpha_error;
			shared_format_of_choice[choice_error_idx][1] = FMT_LUMINANCE_ALPHA;
		}

		// 2 integers can encode as L+L
		float luminance_error = quant_error_rgb + 0 + shared_luminance_error;

		shared_best_error[choice_error_idx][0] = luminance_error;
		shared_format_of_choice[choice_error_idx][0] = FMT_LUMINANCE;
	}
}

Block Mode Iteration

To make full use of the GPU, we process 2 block modes for each block mode iteration. Each processed block mode is handled by 16 threads, which is half the size of the warp. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
unsigned int max_block_modes = bsd->block_mode_count_1plane_selected;
int block_mode_process_idx = 0;
while (block_mode_process_idx < max_block_modes)
{
	__syncwarp();

	int sub_block_idx = tid / 16;
	int in_block_idx = tid % 16;

	int global_idx = sub_block_idx + block_mode_process_idx; // ignore the last block mode for now
	bool is_block_mode_index_valid = (block_mode_process_idx + 1) < max_block_modes;
	if (is_block_mode_index_valid)
	{
		
	}
}

In the arm astc-enc implementation, weight quant errors are computed separately from color endpoint quant errors. The process generates a lot of intermediate buffers. To optimize intermediate buffer usage, we combine the separate passes together and update the total error in-place.

We compute the difference between quanted weights and unquantified weights per thread. The quant error of the block mode is computed by summing the squared texel error using warp reduction.

For each block mode, dispatch four threads to compute the combined error for four endpoint quant formats: integer number 1 to integer number 4. Then, use __shfl_xor_sync to find the best endpoint quant format with minimum error.

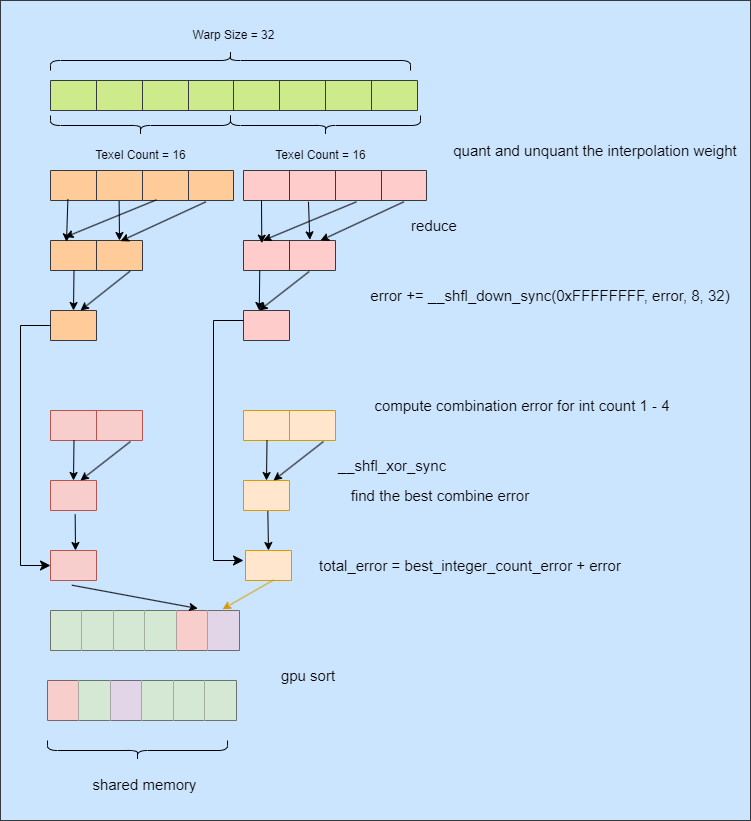
We maintain a shared candidate block mode buffer with 4 actual candidate block modes and 2 block modes updated during each iteration. The last two block modes (4 + 0 and 4 + 1) are used for final GPU sorting.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
if (in_block_idx == 0)
{
	best_integer_count_error = integer_count_error;

	int ql = quant_mode_table[best_integer_count + 1][bitcount];

	uint8_t best_quant_level = static_cast<uint8_t>(ql);
	uint8_t best_format = FMT_LUMINANCE;

	if (ql >= QUANT_6)
	{
		best_format = shared_format_of_choice[ql][best_integer_count];
	}

	float total_error = best_integer_count_error + error;

	candidate_ep_format_specifiers[4 + sub_block_idx] = best_format;
	candidate_block_mode_index[4 + sub_block_idx] = global_idx;
	candidate_color_quant_level[4 + sub_block_idx] = ql;
	candidate_combine_errors[4 + sub_block_idx] = total_error;
}

When current block mode iterations have been completed, perform a GPU sorting. The first four candidate block modes are used in the next pass.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
if (tid < 6)
{
	int num_samller = 0;
	float current_tid_error = candidate_combine_errors[tid];
	float current_ep_format_specifier = candidate_ep_format_specifiers[tid];
	int current_blk_mode_idx = candidate_block_mode_index[tid];
	int current_col_quant_level = candidate_color_quant_level[tid];

	#pragma unroll
	for (int candiate_idx = 0; candiate_idx < 6; candiate_idx++)
	{
		float other_candidate_error = candidate_combine_errors[candiate_idx];
		if ((other_candidate_error < current_tid_error) || ((other_candidate_error == current_tid_error) && (candiate_idx < tid)))
		{
			num_samller++;
		}
	}

	// 0011 1111
	__syncwarp(0x0000003F);
	candidate_combine_errors[num_samller] = current_tid_error;
	candidate_ep_format_specifiers[num_samller] = current_ep_format_specifier;
	candidate_block_mode_index[num_samller] = current_blk_mode_idx;
	candidate_color_quant_level[num_samller] = current_col_quant_level;
}

Find The Best Block Mode

We get four block mode candidates after all block mode iterations are complete. However, to accelerate block mode seraching, the candidate block modes are selected by approximate error instead of the actual difference between the original color and the compressed color. So, in the current pass, we quantify the interpolation weights and color endpoints and compute the exact difference between compressed color and original color.

The exact best block mode is stored in shared memory that will be used in the final block mode compression.

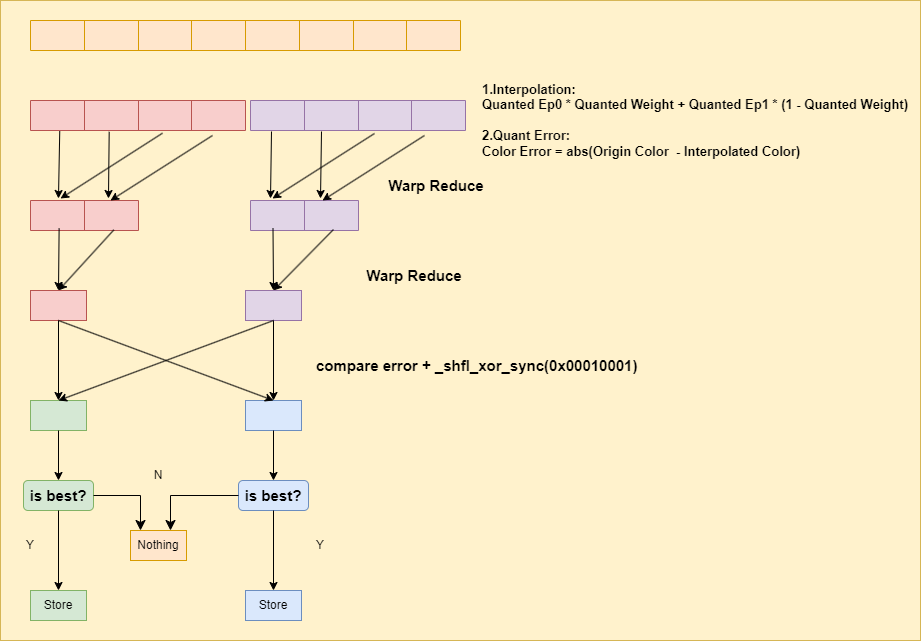
Compress the block mode

The final block mode compression is the same as the CPU-based implementation.

after astc compression:

before astc compression:

GPU ASTC Compression Source Code

ASTC Compression Accleration Using CUDA
http://example.com/2024/06/18/GPU-Based-ASTC-Compression-Using-CUDA/
Author
Shawn Tang
Posted on
June 18, 2024
Licensed under